Binära och hexadecimala talsystemen, vad är det?
Åtta bitar utgör en byte. En bit är den lägsta beståndsdelen i en dator. En bit är en etta eller nolla, strömmen på eller av. Lägre beståndsdel än så kan vi inte hitta i datorn. Ett tecken i datorn är en byte stor (om vi bortser från UTF-8 som är större än en byte för att få plats med specialtecken och svenska tecken exempelvis).
En byte kan maximalt representera talet 255. Det är här det binära talsystemet kommer in i bilden. Om vi tittar på nedanstående bilder så brukar saker och ting falla på plats när det gäller bitar och det binära talsystemet. I bilden direkt nedanför är samtliga bitar (åtta styck) satta till ett. Att alla bitarna är satta till ett innebär att vi adderar ihop alla talen i den nedersta rutan. Vi adderar alltså enbart talen som är “satta”, det vill säga rutorna som har en etta ovanför sig. 111111 binärt är alltså 255 i vårt decimala talsystem.
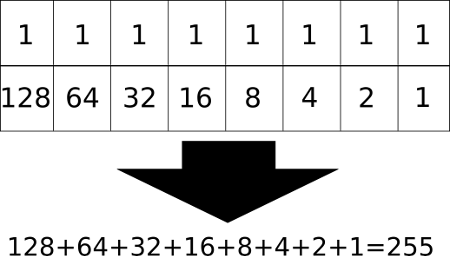
I nästa bild är några bitar “satta”, det vill säga en etta, och några bitar som inte är satta, det vill säga de har en nolla i rutan istället. I just det här fallet med bilden nedan får vi det binära talet 00101011 som decimalt blir 43.
Omvandla från binärt till decimalt
Det enklaste sättet för att omvandla binärt till decimalt är att göra uppställningarna enligt ovan. Man skriver alltså upp det binära talet och under varje siffra skriver vi, med början från höger, 1 2 4 8 16 32 och vidare. Sedan adderar vi bara ihop de tal där vi har en etta. Men varifrån kommer talen 1 2 4 8 16 och 32 ifrån då?
Jo, eftersom det binära talsystemet endast har två möjliga tecken (1 och 0) så säger vi att talsystemet har basen 2. Det är här dessa siffror kommer ifrån, eftersom $2^0 = 1$, $2^1 = 2$, $2^2 = 4$, $2^3 = 8$, $2^4 = 16$, $2^5 = 32$, $2^6 = 64$, $2^7 = 128$ och så vidare. I och med detta kan vi också omvandla från binärt till decimalt på ett annat sätt om vi inte vill skriva ut hela omvandlingen som vi gjorde ovan. Låt oss anta att vi har det binära talet 101100. För att omvandla detta kan vi göra uträkningen enligt nedastående steg. Vi börjar bakifrån som alltid.
\[0\times2^0 = 0\] \[0\times2^1 = 0\] \[1\times2^2 = 4\] \[1\times2^3 = 8\] \[0\times2^4 = 0\] \[1\times2^5 = 32\]Nu adderar vi resultaten och får $4+8+32=44$. Detta sättet kanske är ännu enklare för någon? Det är en smaksak vilket sätt man vill använda, båda bygger dock på samma princip. När vi använder denna metod för att omvanlda behöver vi inte hålla koll på 1, 2, 4, 8 och så vidare, vi ökar bara exponenten med ett för varje siffra.
Omvandla från decimalt till binärt
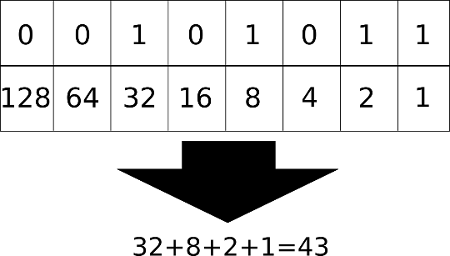
Att göra tvärtom, omvandla decimalt till binärt är inte mycket svårare. Här dividerar vi bara talet med två, noterar resten (1 eller 0), dividerar svaret vi får med två igen, noterar resten igen och så vidare. Om vi tar och testar att omvandla talet 17 till binärt så får vi alltså följande uppställning.
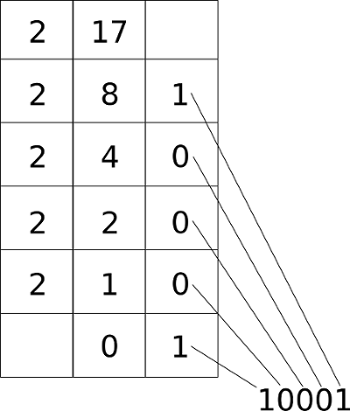
Steg för steg blir uträkningen följande.
\[\frac{17}{2} = 8 + 1 \text{ rest}\] \[\frac{8}{2} = 4 + 0 \text{ rest}\] \[\frac{4}{2} = 2 + 0 \text{ rest}\] \[\frac{2}{2} = 1 + 0 \text{ rest}\] \[\frac{1}{2} = 0 + 1 \text{ rest}\]Svaret blir alltså nu, med början nedifrån, samtliga rester i uträkningarna, 10001. Första siffran i svaret är alltså sista siffran i uträkningen.
Hexadecimala talsystemet
Det hexadecimala talsystemet har 16 som bas, det vill säga det finns totalt 16 olika tecken i talsystemet. Men innan vi går igenom hur man räknar ut hexadecimala värden ska vi reda ut varför det det hexadecimala talsystemet är så frekvent återkommande i datorsammanhang.
Det är nämligen så att det hexadecimala talsystemet gör det enklare att uttrycka större binära tal. Det är faktiskt också mycket enklare att omvandla mellan binärt och hexadecimalt, än vad det är mellan binärt och decimalt. Denna enkelheten kommer ifrån att en grupp om fyra binära tecken är det maximala värdet vi kan uttrycka med ett enda hexadecimalt tecken. För att inte ta miste mellan decimala och hexadecimala tal använder man prefixet 0x framför hexadecimala tal. Det hexadecimala talet 55 skrivs alltså 0x55 för att inte mistas mot det decimala talet 55, som inte är samma värde.
16 möjliga tecken
Det hexadecimala talsystemet har 16 möjliga tecken, alltså 6 fler än i vårt vanliga decimala talsystem. De “extra” tecknen är A-F.
| Hexadecimalt | Decimalt |
|---|---|
| 0x0 | 0 |
| 0x1 | 1 |
| 0x2 | 2 |
| 0x3 | 3 |
| 0x4 | 4 |
| 0x5 | 5 |
| 0x6 | 6 |
| 0x7 | 7 |
| 0x8 | 8 |
| 0x9 | 9 |
| 0xA | 10 |
| 0xB | 11 |
| 0xC | 12 |
| 0xD | 13 |
| 0xE | 14 |
| 0xF | 15 |
Omvandla mellan hexadecimalt och binärt
Att omvandla hexadecimala tal till och från binärt är mycket enkelt. Precis som vi redan har nämnt så handlar det helt enkelt bara om att gruppera de binära talen i grupper om fyra. Detta fungerar åt båda hållen, alltså både när vi ska konvertera till och från binärt.
Vi börjar med några enkla exempel. Vi vet redan att A = 10, B = 11, C = 12, D = 13, E = 14 och F = 15.
Vi börjar med att konvertera 0x2D till binärt.
| Grupp 1 | Grupp 2 |
|---|---|
| 2 | D |
| 10 | 1101 |
0x2D blir alltså 101101 binärt. Vi tar ett lite större tal som nästa exempel, nämligen 0x3CE.
| Grupp 1 | Grupp 2 | Grupp 3 |
|---|---|---|
| 3 | C | E |
| 11 | 1100 | 1110 |
0x3CE i binärt blir alltså 1111001110.
Det är dags att testa att göra tvärtom, omvandla från binärt till hexadecimalt. Detta är precis lika enkelt. Här delar vi bara upp det binära talet i grupper om fyra. Vi börjar med det binära talet 1011101110. Talet innehåller sammanlagt tio siffror, därför börjar vi med att sätta de två första talen för sig själv (10, längst till vänster), sedan delar vi på resten så vi får två grupper om fyra i varje.
| Grupp 1 | Grupp 2 | Grupp 3 |
|---|---|---|
| 10 | 1110 | 1110 |
| 2 | E | E |
1011101110 binärt blir alltså 0x2EE hexadecimalt.
Vi tar ett ännu större binärt tal nu, 1110011011101110110101011. I detta talet har vi 25 tecken. Vi börjar alltså då som vanligt med den första ettan längst till vänster.
| Grupp 1 | Grupp 2 | Grupp 3 | Grupp 4 | Grupp 5 | Grupp 6 | Grupp 7 |
|---|---|---|---|---|---|---|
| 1 | 1100 | 1101 | 1101 | 1101 | 1010 | 1011 |
| 1 | C | D | D | D | A | B |
Lägger vi nu ihop alla de hexadecimala tecken så får vi svaret: 0x1CDDDAB.
Det är just detta som är det fina med det hexadecimala talsystemet, att på ett enkelt sätt och med väldigt få tecken kunna representera stora binära tal.
Omvandla hexadecimala tal till decimala tal
Precis som i vårt vanliga talsystem är positionerna på siffrorna viktiga, exempelvis ental, tiotal, hundratal, tusental och så vidare. Detta bygger på att det decimala talsystemet har 10 som bas, och således har vi 1, 10, 100, 1000 och så vidare. I det hexadecimala talsystemet är istället basen 16, vilket gör att vi istället har ental ($16^0$), sextons ($16^1$), 256:or ($16^2$), 4096:or ($16^3$) och så vidare.
Talet 0x10 blir då 16. Ettan i 0x10 representerar en styck 16 (“sextons”). Nollan efteråt indikerar vi inte ska lägga till några ental. Talet 0x12 blir då 18. Återigen representerar ettan en styck 16. Därefter adderar vi två och får 18.
Talet 0x2C är 44 decimalt. Detta får vi genom att vi nu har två styck 16, alltså $2\times16$ vilket blir 32. Därefter adderar vi C (vilket är 12) till 32, vilket blir 44.
Tabellen nedanför visar de decimala talen mellan 1 och 48 i det hexadecimala talsystemet och hur de räknas fram enligt principen vi precis gått igenom. Notera också att vid varje F har vi en “full grupp” med ettor i det binära talsystemet. Och varje gång vi har en nytt 16:s tal ($1\times16$), ($2\times16$) får vi också ett binärt tal som med ledande ettor och resten nollor. Det finns många mönster att upptäckta i tabellen här nedan, allting hänger ihop.
| Hexadecimalt | Uträkning till dec | Decimalt | Binärt |
|---|---|---|---|
| 0x1 | $1$ | 1 | 1 |
| 0x2 | $2$ | 2 | 10 |
| 0x3 | $3$ | 3 | 11 |
| 0x4 | $4$ | 4 | 100 |
| 0x5 | $5$ | 5 | 101 |
| 0x6 | $6$ | 6 | 110 |
| 0x7 | $7$ | 7 | 111 |
| 0x8 | $8$ | 8 | 1000 |
| 0x9 | $9$ | 9 | 1001 |
| 0xA | $9+1$ | 10 | 1010 |
| 0xB | $9+2$ | 11 | 1011 |
| 0xC | $9+3$ | 12 | 1100 |
| 0xD | $9+4$ | 13 | 1101 |
| 0xE | $9+5$ | 14 | 1110 |
| 0xF | $9+6$ | 15 | 1111 |
| 0x10 | $(1\times16^1)+0$ | 16 | 10000 |
| 0x11 | $(1\times16^1)+1$ | 17 | 10001 |
| 0x12 | $(1\times16^1)+2$ | 18 | 10010 |
| 0x13 | $(1\times16^1)+3$ | 19 | 10011 |
| 0x14 | $(1\times16^1)+4$ | 20 | 10100 |
| 0x15 | $(1\times16^1)+5$ | 21 | 10101 |
| 0x16 | $(1\times16^1)+6$ | 22 | 10110 |
| 0x17 | $(1\times16^1)+7$ | 23 | 10111 |
| 0x18 | $(1\times16^1)+8$ | 24 | 11000 |
| 0x19 | $(1\times16^1)+9$ | 25 | 11001 |
| 0x1A | $(1\times16^1)+10$ | 26 | 11010 |
| 0x1B | $(1\times16^1)+11$ | 27 | 11011 |
| 0x1C | $(1\times16^1)+12$ | 28 | 11100 |
| 0x1D | $(1\times16^1)+13$ | 29 | 11101 |
| 0x1E | $(1\times16^1)+14$ | 30 | 11110 |
| 0x1F | $(1\times16^1)+15$ | 31 | 11111 |
| 0x20 | $(2\times16^)+0$ | 32 | 100000 |
| 0x21 | $(2\times16^1)+1$ | 33 | 100001 |
| 0x22 | $(2\times16^1)+2$ | 34 | 100010 |
| 0x23 | $(2\times16^1)+3$ | 35 | 100011 |
| 0x24 | $(2\times16^1)+4$ | 36 | 100100 |
| 0x25 | $(2\times16^1)+5$ | 37 | 100101 |
| 0x26 | $(2\times16^1)+6$ | 38 | 100110 |
| 0x27 | $(2\times16^1)+7$ | 39 | 100111 |
| 0x28 | $(2\times16^1)+8$ | 40 | 101000 |
| 0x29 | $(2\times16^1)+9$ | 41 | 101001 |
| 0x2A | $(2\times16^1)+10$ | 42 | 101010 |
| 0x2B | $(2\times16^1)+11$ | 43 | 101011 |
| 0x2C | $(2\times16^1)+12$ | 44 | 101100 |
| 0x2D | $(2\times16^1)+13$ | 45 | 101101 |
| 0x2E | $(2\times16^1)+14$ | 46 | 101110 |
| 0x2F | $(2\times16^)+15$ | 47 | 101111 |
| 0x30 | $(3\times16^1)+0$ | 48 | 110000 |
I tabellen nedan visas några större hexadecimala tal som 0x10, 0x100, 0x200, 0xFFFF och så vidare som har stor betydelse i datorsammanhang. Här ser vi ytterligare mönster och får en känsla för hur allting hänger ihop.
| Hexadecimalt | Uträkning till dec | Decimalt | Binärt |
|---|---|---|---|
| 0x40 | $(4\times16^1)+0$ | 64 | 1000000 |
| 0x80 | $(8\times16^1)+0$ | 128 | 10000000 |
| 0x100 | $(1\times16^2)+0$ | 256 | 100000000 |
| 0x200 | $(2\times16^2)+0$ | 512 | 1000000000 |
| 0x400 | $(4\times16^2)+0$ | 1024 | 10000000000 |
| 0x800 | $(8\times16^2)+0$ | 2048 | 100000000000 |
| 0x1000 | $(1\times16^3)+0$ | 4096 | 1000000000000 |
| 0x8000 | $(8\times16^3)+0$ | 32768 | 1000000000000000 |
| 0xFFFF | Se nedan* | 65535 | 1111111111111111 |
| 0x10000 | $(1\times16^4)+0$ | 65536 | 10000000000000000 |
* 0xFFFF till decimalt: $(15\times16^3)+(15\times16^2)+(15\times16^1)+(15\times16^0)$
Räkna ut större och mer komplicerade tal
Hur omvandlar vi då större och mer komplicerade hexadecimala tal till decimalt? Vi utgår från samma princip som ovan och adderar resultaten. Vi tar 0x5CE som exempel.
Vi börjar bakifrån med siffran E eftersom det då är enklare att hålla ordning på exponenten. Kom ihåg att E motsvarar 14 och C motsvarar 12.
\[14\times16^0=14\] \[12\times16^1=192\] \[5\times16^2=1280\]Nu adderar vi ihop resultaten: $14+192+1280=1486$. Notera att detta var exakt samma princip vi använde när vi omvandlade binära tal till decimala tal, fast istället för basen 2 använde vi basen 16. Återigen, allting hänger ihop.
Nyhetsbrev
Nyhetsuppdateringar från tidningen direkt till din inkorg, helt kostnadsfritt. Avsluta när du vill.
Relaterade artiklar
-
Använd bc för att omvandla talsystem
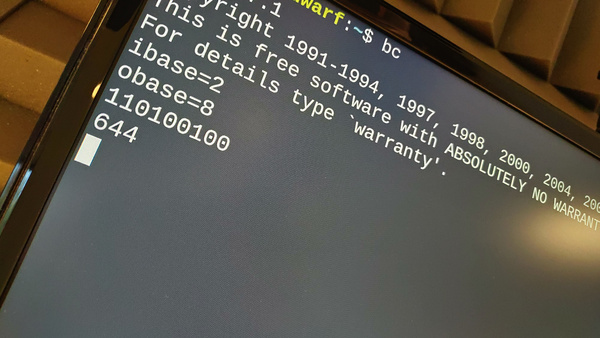
Att kunna omvandla mellan olika talsystem med papper och penna är bra att kunna. Men ibland behöver vi bara ett svar – snabbt. Det här kan programmet
bchjälpa dig med. Programmetbcfinns i de flesta Unixliknande system, så som Linux, FreeBSD, macOS med flera. Förkortningenbcstår för Basic Calculator men benämns även Bench Calculator. -
Hur procent och bråktal hänger ihop

Procenttal kan skrivas som bråktal och vice versa. Att skriva om procent till bråktal kan därför hjälpa förståelsen för hur man räknar med procent.
-
Roliga egenskaper hos polygoner

Det finns många roliga och intressanta egenskaper hos polygonerna. Det mest intressanta är kanske polygonernas vinkelsumma, och hur dessa kan räknas fram genom att rita trianglar inuti polygonerna.
-
Python och trigonometri

Lite uppfräschning av trigonometri och Python är aldrig fel. Här får vi lära oss hur man kan rita upp rätvinkliga trianglar – direkt i Python – om vi känner till två av sidorna. För detta kommer vi att använda modulerna turtle och math.
-
Ett av mina första nyttoprogram

Vilken nostalgi det var när jag gick igenom programmen på min gamla grafräknare från gymnasiet, en TI-83. Där hittade jag ett av mina första nyttoprogram jag någonsin skrivit. Det var ett program skrivit i ett språk kallat TI-BASIC, en version av Basic för Texas Instruments grafräknare. Året då jag skrev programmet är troligen år 2000 eller 2001.
Senaste nyheterna och inläggen
-
GrapheneOS – mer än bara ett säkert mobil-OS

GrapheneOS är ett operativsystem för Google Pixel-telefoner baserat på Android men utvecklat helt fristående från Google. Det är ett renare och betydligt säkrare system än vanliga Android.
-
Avlyssna trafik på servern med Wireshark och TShark
Wireshark är ett ovärderligt verktyg för att felsöka nätverkskonfigurationer, applikationer, API:er, demoner och mycket annat. I kombination med
tsharkkan vi dessutom avlyssna trafiken på en server i realtid. -
Mysig stämning på sommarens första demoparty

I helgen var det Reunion 2024 i Kvidinge Folkets hus, sommarens första skånska demoparty. Partyt organiserades av Jesper “Skuggan” Klingvall. På plats fanns ett 30-tal besökare.
-
Sommarens skånska demopartyn

Årets sommar bjuder på två skånska demopartyn. Först ut är Reunion i Kvidinge den 28–30 juni. Därefter är det Pågadata i Örtofta den 9–11 augusti.
-
Riskerna med BankID som ingen pratar om

BankID är ett säkert och smidigt sätt att identifiera sig online. Men i takt med dess ökade popularitet och användning har det blivit en svag länk – en single point of failure – på mer än ett sätt.
Utvalda artiklar
-
Mysig stämning på sommarens första demoparty

I helgen var det Reunion 2024 i Kvidinge Folkets hus, sommarens första skånska demoparty. Partyt organiserades av Jesper “Skuggan” Klingvall. På plats fanns ett 30-tal besökare.
-
Datorparty i Landskrona

I helgen höll Syntax Society sitt årliga sommarparty. Platsen var en källarlokal i Landskrona där ett femtontal personer medverkade.
-
Det första Pågadata har ägt rum

I helgen ägde det första Pågadata rum – uppföljaren till Gubbdata. Platsen var Folkets Hus i Kvidinge. Organisatör av partyt var Johan “z-nexx” Osvaldsson med hjälp från Jesper “Skuggan” Klingvall. Partyt hade över 100 anmälda deltagare.
-
Även hovrätten fäller poliserna för att ha satt dit oskyldig

Hovrätten fastställer straffet för de två poliser som förra året dömdes till vardera ett års fängelse av Lunds tingsrätt för att ha misshandlat och satt dit en oskyldig man. De båda poliserna ska även betala skadestånd till mannen.
-
Retroloppis i Påarp

Idag var det retroloppis hos Andreas Nilsson i Påarp. På baksidan av huset fanns hundratals spel uppradade på långa bord. Trots friska vindar och sval temperatur var loppisen välbesökt.
